Tecniche di sintesi: Phase Vocoder

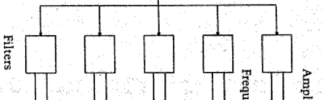
Il Phase Vocoder è uno dei più noti metodi di analisi/risintesi dello spettro sonoro che sviluppa, in ambito digitale, i concetti già adottati con il VOCODER di Homer Dudley. Tradizionalmente adottato per i segnali vocali, il Phase Vocoder, similmente al dispositivo analogico, è strutturato in due sezioni utili rispettivamente all’analisi e alla sintesi.

Le origini negli anni Sessanta

Una prima versione del Phase Vocoder è stata sviluppata nel 1966 da James Flanagan e Roger Golden, ricercatori ai Laboratori Bell, dove Dudley aveva messo a punto il Vocoder. Il principio da cui partirono i due ricercatori era che facendo passare un segnale sonoro attraverso una batteria di filtri in parallelo non si comprometteva la qualità del segnale in uscita. Su questa intuizione, in verità, si fonda anche il Vocoder. Mentre quest’ultimo consentiva, per ciascun filtro, esclusivamente la trasmissione dei valori di ampiezza, la tecnica adottata da Flanagan e Golden si estendeva anche alla trasmissione della fase, da cui il nome Phase Vocoder.

Le simulazioni con IBM-7094

In realtà, rispetto alle intenzioni iniziali, il risultato finale della ricerca non fu soddisfacente. Riuscirono nell’intento di migliorare il processo di sintesi, quindi la qualità del segnale sonoro, tuttavia l’insieme dei dati raccolti durante il processo di analisi restituivano un file con dimensione maggiore di quella del segnale originale. Sul piano pratico questo comportava un notevole sforzo computazionale. La prima simulazione al computer fu condotta con un IBM 7094 e un software realizzato con il linguaggio BLODI-B, sviluppato appositamente per processare segnali di parlato digitalizzato.
La difficoltà nella gestione dei dati rese difficile, per diversi anni, l’utilizzo del Phase Vocoder. In seguito, verso la metà degli anni Settanta, il ricercatore Portnoff sviluppò un Phase Vocoder ancora più efficiente implementando al suo interno la Fast Fourier Transform.

Analisi e sintesi con il Phase Vocoder

Come nel VOCODER, anche nel Phase Vocoder il passaggio del segnale originale avviene all’interno di una batteria di filtri posti in parallelo, tale da coprire l’intera larghezza di banda del segnale originale. In questo caso i filtri permettono di misurare sia l’ampiezza sia la fase di ciascun suono sinusoidale per ciascuna banda di frequenza. Questa si definisce la fase di analisi. Da questi valori si ricavano due inviluppi: per l’ampiezza e per la frequenza. Durante la fase di sintesi, i dati ottenuti con l’analisi si possono sia lasciare invariati (in questo modo, teoricamente, avremo un segnale identico a quello originale), sia modificarli (ad esempio agendo sui due inviluppi), per ottenere risultati timbrici differenti.

La fase di analisi del Phase Vocoder

Ai fini del risultato finale, la fase dell’analisi è di estrema importanza, per questo è necessario prestare particolare attenzione all’insieme dei parametri definiti dall’utente. La scelta di questi parametri (Frame Size – Window – FFT Size – Hop Size), andrebbe valutata sia in base alle qualità intrinseche al segnale originale, sia in base alle caratteristiche che dovrebbe avere il suono risintetizzato. In generale vale ricordare la regola che migliore sarà l’analisi e tanto più simile all’originale sarà il suono sintetizzato. La fase di analisi si svolge prendendo in considerazione due elementi in particolare: la frequenza e il tempo. Per quanto riguarda la frequenza, bisogna ricordare che durante l’analisi lo spettro del segnale originale viene suddiviso in canali di frequenza, dove la larghezza di banda di ciascun canale si calcola suddividendo la frequenza di campionamento per il frame size. Il numero dei canali, che è strettamente connesso alle caratteristiche del segnale originale, è ottenuto suddividendo la frequenza di campionamento per la frequenza fondamentale del segnale.

Dimensioni del Frame (Frame Size)

La grandezza del frame è uno dei parametri più importanti per lo svolgimento di una buona analisi. Va ad incidere, in particolare, sulla frequenza e sul tempo. La dimensione di ciascun frame, che si misura in numero di campioni utilizzati, sarà obbligatoriamente un numero intero potenza di 2 (64, 128, 256 campioni, etc.). Per quanto riguarda la frequenza, possiamo dire che dalla grandezza del frame dipende il numero di frequenze del segnale originale conservate, quindi la sua risoluzione in termini di frequenza. In altri termini vuol dire che più alto è il valore del Frame Size più alto sarà anche il numero delle frequenze, e viceversa. Se volessimo, ad esempio, analizzare un suono che viaggia su ottave molto basse, dove è più difficoltosa la selezione delle frequenze, allora tenderemo ad impostare un Frame Size abbastanza alto per avere una maggiore accuratezza delle frequenze presenti. L’importanza di questo parametro agisce anche sulla risoluzione del tempo. Se in precedenza si è detto che lo spettro viene suddiviso in canali di frequenza, va aggiunto che il segnale originale viene suddiviso anche in porzioni di tempo. A differenza del caso precedente, però, per ottenere una buona risoluzione temporale è necessario mantenere basso il valore del Frame, per motivi che vedremo in seguito. Per il momento è sufficiente ricordare che in base al Frame Size, più dettagliata sarà l’analisi delle frequenze, più grossolana sarà quella del tempo e viceversa.

Tipologia di finestra (Window Type)

La scelta del tipo di finestra diventa molto importante quando si desidera fare un’analisi molto accurata, visto che ciascuna finestra tende ad introdurre delle distorsioni, quindi ad alterare il processo di analisi. Solitamente, oggi, qualsiasi Phase Vocoder permette la scelta di finestre standard come quella di Hamming, Hanning, Gaussian troncata, Blanckman-Harris o Kaiser.

Dimensioni della FFT (FFT Size)

La scelta di questo valore dipende dal grado di trasformazione che vogliamo esercitare sul segnale originale. Il valore deve essere un numero intero potenza di due, in maniera che sia almeno il doppio del Frame Size. Dal momento che la grandezza della FFT incide sulle prestazioni del processore e dal momento che il suo valore è strettamente connesso a quello del Fram Size, capiamo quanto la scelta di quest’ultimo sia importante anche per la FFT.

Fattore Hop (Hop Size)

Il fattore HOP è definito anche fattore di sovrapposizione delle finestre. Determina il numero di campioni che, durante l’analisi, vengono saltati ogni qualvolta viene effettuata una nuova misurazione dello spettro. Quanto più è piccolo questo valore tanto più sovrapposte saranno le finestre successive. Non va dimenticato che per la risintesi è necessario un numero minimo di sovrapposizioni (circa otto).

Applicazioni del Phase Vocoder

Al di là di quanto possa essere approfondito lo studio di questi parametri o il ragionamento sulla loro scelta, non bisogna dimenticare un’indicazione di carattere generale tutt’altro che indifferente: non esistono dei valori che si possano considerare indicati per qualsiasi situazione. Certamente all’interno di certi range possiamo trovare dei valori che si possono considerare accettabili per una maggiore varietà di situazioni ma resta il fatto che ogni segnale sonoro in ingresso richiede un’analisi studiata caso per caso. Pur essendo un metodo molto utilizzato perché efficiente, va sottolineato che il Phase Vocoder è anche tra i metodi più impegnativi in termini di computazione, per questo si sono sviluppate anche diverse modalità che consentono di ridurre le dimensioni del file di analisi.
Tra i tanti compositori che hanno fatto uso del Phase Vocoder, ricordiamo in particolare Charles Dodge e Trevor Wishart, che più di altri hanno dimostrato interessanti applicazioni musicali di questo metodo. Mark Dolson, infine, verso gli inizi degli anni Ottanta, si è occupato di implementare la tecnica del Phase Vocoder anche all’interno del Sistema CARL di Richard Moore e Gareth Loy.

Se vuoi approfondire questo argomento, ti suggerisco la lettura dei seguenti argomenti: John Gordon, John Strawn, An Introduction to the Phase Vocoder, Proceedings, CCRMA, Department of Music, Stanford University, February 1987. Poi James Flanagan, Roger Golden, Phase Vocoder, The Bell System Technical Journal, Novembre 1966. Infine Curtis Roads, The Computer Music Tutorial, MIT Press, 2004.